Eric Ries over at TechCrunch recently wrote an article discussing racism/sexism in Silicon Valley and the technology industry. The article discusses differences in aptitude between men and women, and attempts to downplay them as the cause of a lack of women in technology (and at YC-funded companies, specifically):
Could this be the result of innate differences between white men and other groups? The math simply doesn’t hold up to support this view. Think about two overlapping populations of people, like men and women. They would naturally be normally distributed in a bell curve around a mean aptitude. So picture those two bell curves. Here in Silicon Valley, we’re looking for the absolute best and brightest, the people far out on the tail end of aptitude. So imagine that region of the curve. How far apart would the two populations have to be to explain YC's historical admission rate of 4% women? It would have to be really extreme.
It looks like Eric Ries didn't actually do the math.
According to the most recent data, men and women have more or less identical mean aptitude for mathematics. But there is a considerable difference in the variance - men's aptitude has a variance 11-20% higher than women's. I.e., the population distributions look like this (splitting the difference and taking men's variance to be 16% higher):
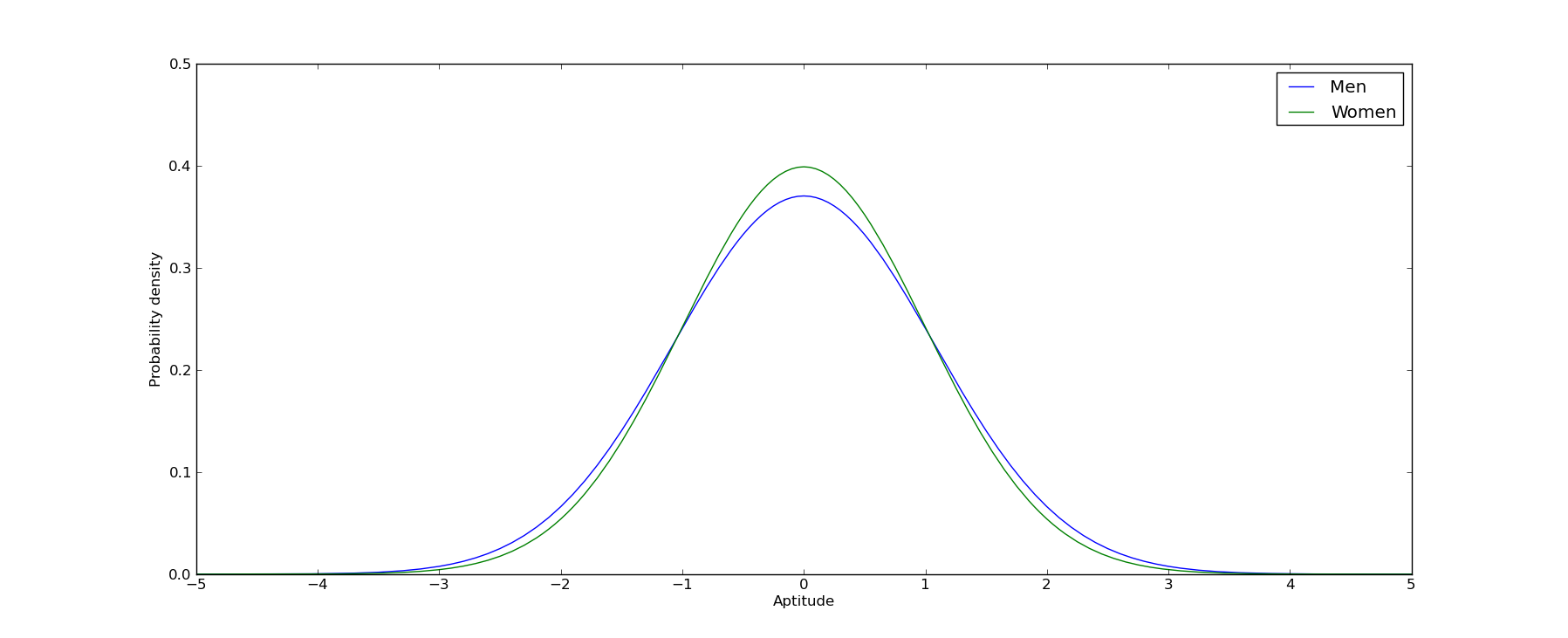
Doesn't look like a "really extreme difference", right? It's not.
But lets zoom in on people who are in the top 2.5% in mathematical ability alone, i.e. people with the capability to be decent programmers:
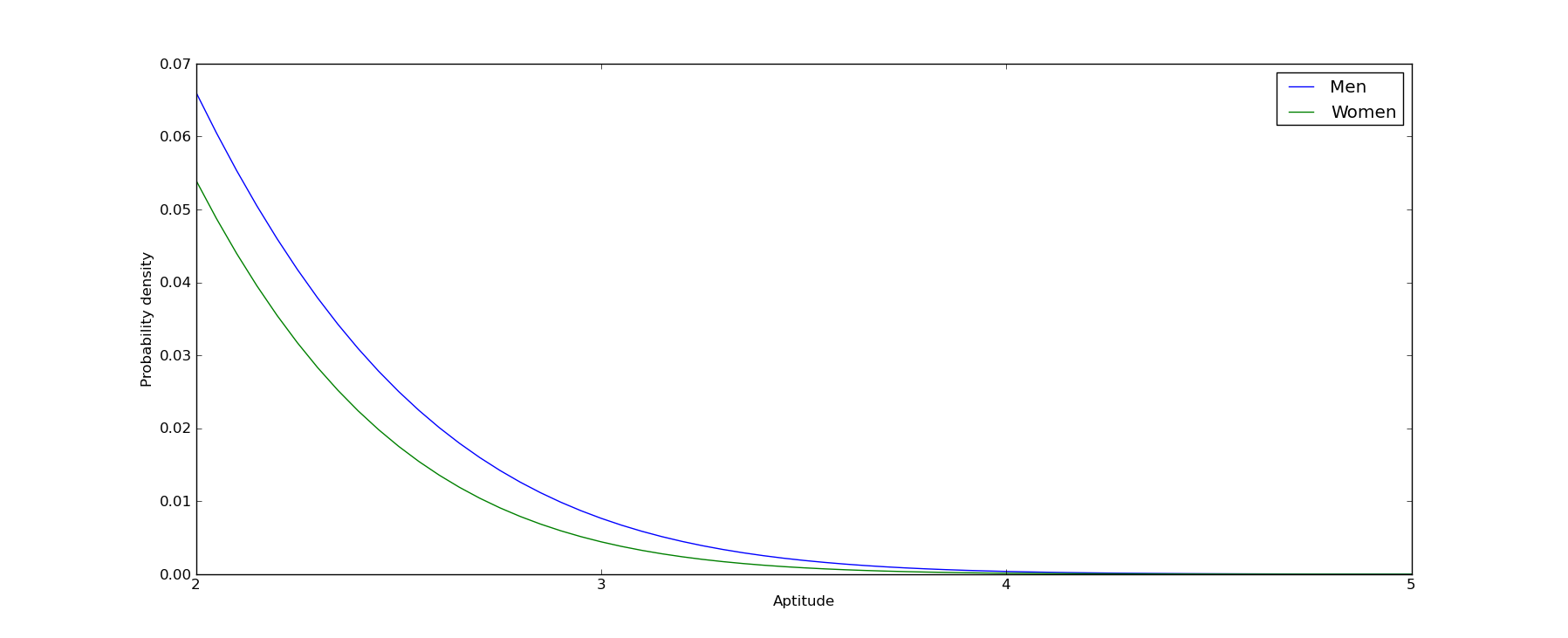
In this case, men make up 58% of the total. If we zoom in to people who are 1 in 1000, i.e. people with the programming aptitude for YCombinator, we find men make up 67.5% of this population.
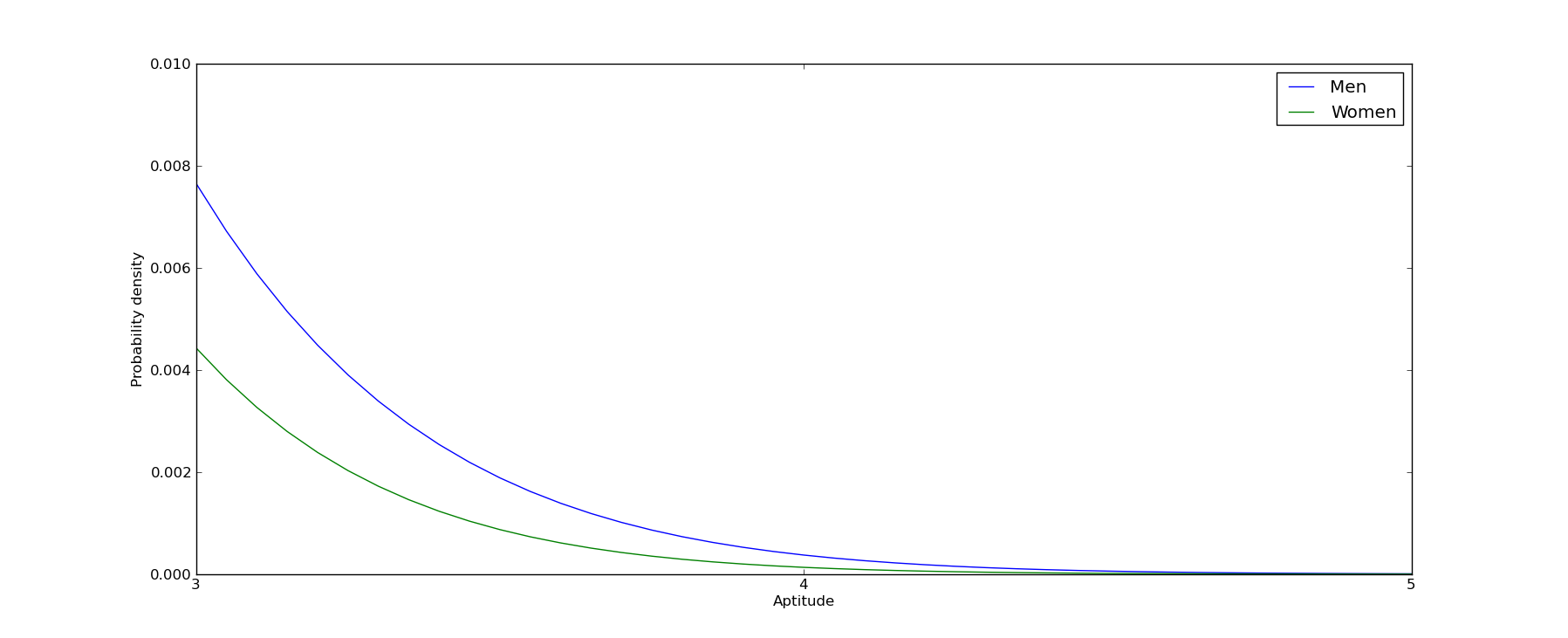
Small differences in mathematical ability alone can add up to a lot, at least among smart people.
Eric Ries further goes on to present some numbers:
We all know there is a huge gender gap in computer science. But that gap means that women receive only about 30% of degrees in CS. But 30% is a lot larger than 4%; and that's a big math problem for advocates of the pipeline theory.
It's true - if YCombinator looks only for mathematical ability which is 1 in 1000, then women should be closer to 30%. But YCombinator isn't Putnam - they look for more than just raw math ability.
But mathematical ability is clearly not the only thing they look for. Suppose, hypothetically, that "business aptitude" is also distributed the same way as math ability - identical mean, marginally different variance. Suppose it's also statistically independent of mathematical ability, and assume YCombinator wants a person who is top 0.1% in business sense.
At this point, the pool is up to 81% men purely on the basis of aptitude in two separate traits.
Unlike aptitude, men and women actually display large differences in risk aversion. For example, one study shows that out of a sample of MBA students, 57% of men are willing to pursue a risky career in finance, compared to only 36% of women. Assuming the same probabilities apply to men and women with aptitude sufficient for YCombinator, then the set of people with sufficient aptitude and attitude would be 87% men.
Small differences in the distributions of men and women don't allow you to predict much about any individual trait of a randomly selected individual. But when you limit yourself to the far tails of probability distributions, they do.
At this point, we cannot pin down any specific innate differences that explain precisely why YCombinator has so few female-founded companies. I'm not attempting to claim science currently knows everything about this topic. The only point I'm making is that it does not take "really extreme" differences in aptitude or innate preferences to account for gender differences in high end professions. It just takes a few small differences chained together.