Here's a scenario that I believe to be common. I've got a dataset I've been collecting over time, with features \(x_1, \ldots, x_m\) This dataset will generally represent decisions I want to make at a certain time. This data is not a timeseries, it's just data I happen to have collected over time. I will call this the old data and old features.
The problem I'm interested in right now is the situation where some of the data was not collected since the beginning of time. I will assume that on a much smaller dataset - e.g. the most recent 10-20% of the data - I have collected additional features \(x_{m+1} \ldots x_m\) which I have reason to believe are useful for predictions. I will call this the new data and new features.
The challenge here is that if we combine the training data into a single table, it looks something like this:
| x1 | x2 | Xn+1 | Xn+2 | y |
|---|---|---|---|---|
| 5 | -3 | null | null | False |
| 7 | 2 | null | null | True |
| . | 0 | . | . | . |
| 3 | 5 | 0.2 | -0.5 | False |
| 4 | -6 | 0.9 | 1.2 | True |
This dataset is not representative of future data; future data will not have nulls in the columns representing the new features.
It is my desire to build a scheme for transfer learning using non-neural network methods such as XGB. Specifically, I want to train a model on the large dataset using only the old features, then transfer knowledge gained in this way to a model trained on the small dataset and including the new features. In this blog post I provide a proof of concept on that classical boosting provides a mechanism for accomplishing this knowledge transfer.
Concrete example: standard stock market data, e.g. end of day prices, along with data pulled out of assorted EDGAR documents. This data is generally available as far back as I'd like, provided I'm willing to parse old SEC files or pay a data provider for it. I also have some alternative data which only goes back a couple of years. I believe it is customary to pretend this is satellite photos of cars in walmart parking lots rather than badly anonymized data about consumers purchased from VISA or T-Mobile which consumers would generally expect to be kept confidential.
Standard options include:
- Training a model on all rows, including rows for which the new data is null.
- Training a model only on the new data.
A significant problem with (1) is that the model can learn spurious correlations between missingness and outcomes - e.g. if one starts collecting new data during a bear market, the model may learn "data present = stonks go down". The key problem with (2) is that the size of the new dataset might just be too small.
Alternate setup: Trunk and Branch Models
Another way to think about this setup for the dataset is via the concept of "trunk and branch" models. One has a large dataset - in the neural network context this is typically a large corpus of language or images. One also has a smaller set of data, either significantly more specialized or ith additional data (such as annotations) and which is representative of the problem one actually wishes to solve.
Concrete example: the large dataset might be a corpus of all kinds of scraped data - journalism, blog posts, tumblr, etc. The smaller dataset might be language from a very specific domain with more limited language and a narrow goal - SEC reports, restaurant reviews, etc. The trunk and branch model involves training a trunk model on the full dataset and a branch model on the narrow dataset.
The purpose of the trunk model is to learn things of general applicability - how the English language works. The purpose of the branch model is to actually predict an outcome of interest - e.g. XYZ company has reported impairment of goodwill, material control weaknesses, or perhaps behaviors indicating earnings management. Additional features present in the narrow dataset may be things like various annotations and structured data which SEC reports tend to contain (SEC-flavored XBRL FTW!).
In mathematical terms this is identical to the setup above. The "new" data is the narrow dataset on which we actually want to make useful predictions, whereas the "old" data is the larger corpus of language in general. Although I am not making any use of this neural network mathematical framework here, this general idea did inspire my approach a bit.
My proposed method: boosting across datasets
I propose a method I haven't seen described elsewhere, but which I've been having some success with: boosting a model trained on old data to the new data. Code used in this blog post is available on github. The idea is as follows.
First, train a model on old data, which by necessity doesn't use new features. Call this the "old model".
Second, compute model scores on the new data. Then compute model weights which are large in places where the old model got things wrong, low otherwise. Adaboost weighting provides a great template for this.
Finally, train a model on the new data using the weights from the previous step. Final scores are merely the sum of the scores of the individual models.
This procedure probably seems familiar because it is - it's almost exactly the same as ordinary boosting. But with classical boosting we're taking a weak learner and repeatedly training new models on the same data to address weaknesses in the learner. In contrast, I'm taking a (hopefully!) stronger learner and training a single new model on different data to address weaknesses in the dataset itself.
Avoiding confusion: For clarity of exposition I am being intentionall vague about which specific model I'm using. That's because the model I choose to use is gradient boosting and I don't want to conflate boosting across datasets with boosting on a fixed dataset. Additionally, in the example code I provide, that's all handled within libraries and there's no compelling reason it couldn't be swapped out for a different method.
Concrete details
I will now include some (slightly oversimplified) pseudocode to illustrate the details. Real code is in the github repo.
The weight computation is a simplified version of adaboost weights taken directly from the sklearn implementation, and simplified slightly to the case of binary classifiers:
def adaboost_weights(estimator, X, y, learning_rate=0.5, sample_weight=None):
"""Implement weights for a single boost using the SAMME.R real algorithm."""
y_predict_proba = estimator.predict_proba(X)
if sample_weight is None:
sample_weight = np.ones(shape=y.shape) / len(y)
n_classes = 2
classes = np.array([0,1])
y_codes = np.array([-1.0 / (n_classes - 1), 1.0])
y_coding = y_codes.take(classes == y[:, np.newaxis])
# Displace zero probabilities so the log is defined.
# Also fix negative elements which may occur with
# negative sample weights.
proba = y_predict_proba # alias for readability
np.clip(proba, np.finfo(proba.dtype).eps, None, out=proba)
# Boost weight using multi-class AdaBoost SAMME.R alg
estimator_weight = (
-1.0
* learning_rate
* ((n_classes - 1.0) / n_classes)
* xlogy(y_coding, y_predict_proba).sum(axis=1)
)
# Only boost positive weights
sample_weight *= np.exp(
estimator_weight * ((sample_weight > 0) | (estimator_weight < 0))
)
return sample_weight
Note that the learning_rate parameter is just something I picked arbitrarily after fiddling around in a notebook.
It could almost certainly be chosen more robustly.
The model computation is then pretty straightforward, exactly as described above:
old_idx = (train_X['old_data'] == 1)
pipe1 = build_pipeline(train_X[old_idx])
pipe1.fit(train_X[old_idx], train_y[old_idx])
sample_weight = adaboost_weights(
pipe1, train_X[~old_idx].copy(),
train_y[~old_idx].copy(),
learning_rate=0.25,
sample_weight=base_weights,
)
pipe2 = build_pipeline(train_X[~old_idx])
pipe2.fit(
train_X[~old_idx],
train_y[~old_idx],
final_estimator__sample_weight=sample_weight
)
boosted_pipe = SummedPredictors([pipe1, pipe2], [1.0, 1.0])
Similarly, the weight on the second predictor is chosen arbitrarily here to be 1.0. This is again a parameter which should be tweaked
to see if improvements can be gained.
The exact code can be found in the notebook, this version removes some irrelevant details for brevity.
The function build_pipeline in the code sample above can be found on github
and is basically just the minimal sklearn pipeline needed to pipe the dataset into sklearn.ensemble.HistGradientBoostingClassifier.
If you are a reader considering using this method for your own dataset, I encourage you to simply use your own pipeline in place of my build_pipeline method -
it will almost certainly work better for your data. There's one modification I would suggest making - if your current pipeline uses some variant of
sklearn.impute.MissingIndicator to handle the nulls in the new features, I would suggest removing it for obvious reasons.
How I'll test this method
I've constructed several datasets, some synthetic, some taken from kaggle competitions or standard sklearn test datasets.
All datasets are binary classifiers, i.e. the target is in {0,1}.
| name | data_source | data drift | num_rows |
|---|---|---|---|
| santander | https://www.kaggle.com/competitions/santander-customer-satisfaction | False | 38010 |
| car_insurance | https://www.kaggle.com/datasets/ifteshanajnin/carinsuranceclaimprediction-classification | False | 58592 |
| tabular_playground | https://www.kaggle.com/competitions/tabular-playground-series-aug-2022/data?select=train.csv | False | 26570 |
| synthetic_1 | sklearn.datasets.make_classification | False | 100000 |
| synthetic_2_dataset_shift | sklearn.datasets.make_classification | True | 100000 |
| cover_type_dataset_shift | sklearn.datasets.fetch_covtype, modified | True | 581012 |
In all cases I'm then modifying the data along the following lines (with minor changes made for a few datasets):
X['old_data'] = bernoulli(old_data_size).rvs(len(X))
...
train_X, test_X, train_y, test_y = train_test_split(X, y, train_size=0.75)
for c in train_X.columns:
if (bernoulli(old_data_drop_frac).rvs() == 1) and (c != 'old_data'):
train_X.loc[train_X['old_data'] == 1, c] = None
Specifically I'm declaring a significant fraction of the data to be "old". Then in the old data I'm nullifying some columns.
In all cases I've adjusted the datasets to have 2 classes, even though some have more (e.g. fetch_covtype has 7). In these
cases I'm arbitrarily mapping some of the outcomes to 0 and some to 1. This is for convenience, there's nothing fundamental
to the method which requires this.
In the performance simulations I am then varying several parameters:
- I vary the fraction of the dataset corresponding to the old data, from 10% to 95%.
- I vary which columns are dropped at random.
This means that for each parameter choice, I retrain multiple models on different datasets.
Dataset drift
In some cases I've introduced data drift as well. Data drift is modeled by introduced a third class in the data generation. Rows corresponding to this class are present only in the new data (and test data). This is intended to model the scenario when in addition to collecting new data, the dataset also changes with time and the training set is not perfectly representative of the test data.
For example, in the sklearn.datasets.fetch_covtype, modified data source, I mapped cover types {0,1} -> 0 and
{2,3,4,5,6}->1. Cover type 6 was used for dataset drift and was excluded from old data.
Computing "regret"
In order to get a baseline on how accurate a model could be absent all this dataset fuckery, I also trained a model on the same datasets but without dropping any data. I am defining the "regret" as the difference in roc_auc between this "best possible" model and the results of models trained on data with columns partially dropped.
Note that this differs a bit from the concept of decision theoretic regret. I am sure there might be a better name for it, I just don't know what it is.
Results
Here's a graph of simulations illustrating what one might expect from this method, across various scenarios.
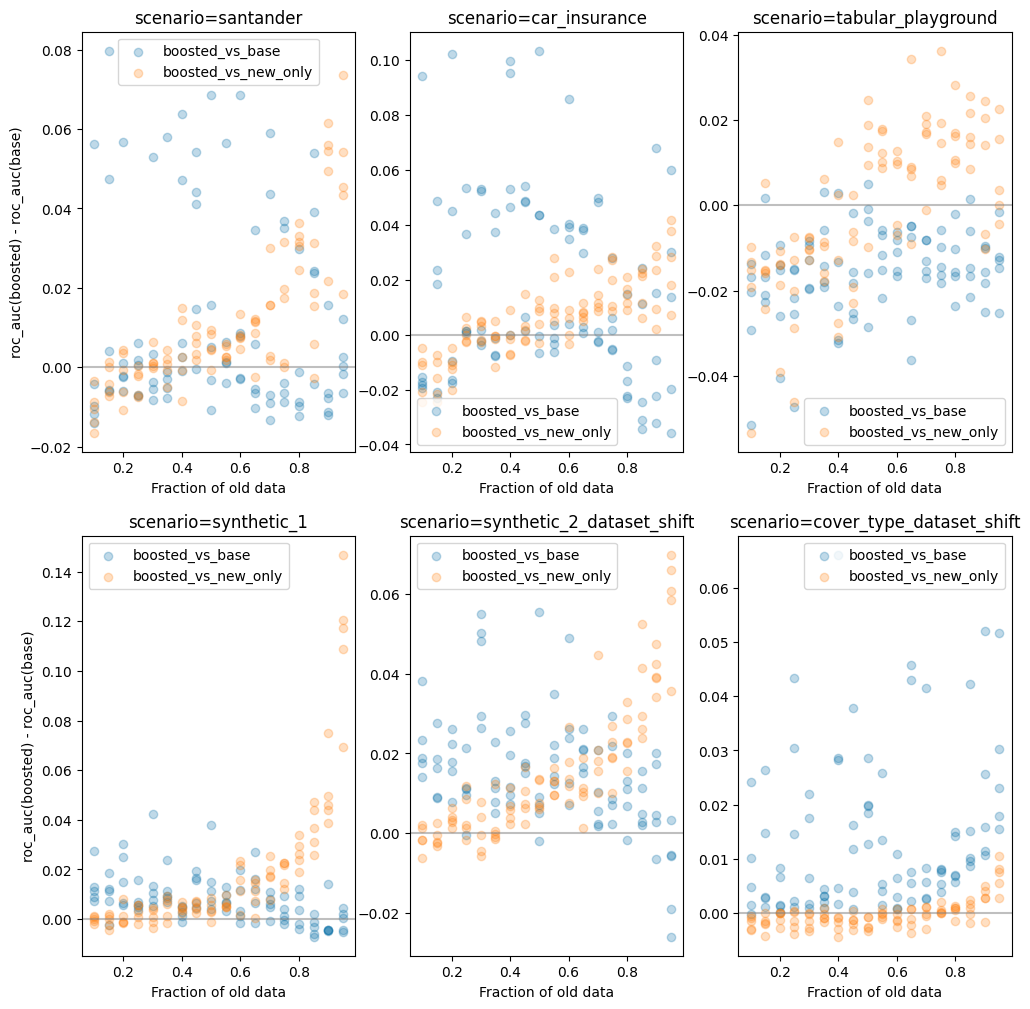
The x-axis of the graph consists of different sizes of the old dataset, ranging from 10% to 95%. The Y-axis represents the delta in model performance (roc_auc) between the boosted model and the two baselines - training on the full dataset (blue) and training on new data only (orange).
Different dots at the same x-value correspond to different (randomized) choices of which columns should be deleted.
There is of course a wide range of performance, as one might expect. If randomly nullifying columns deletes important model features then we expect performance to go down significantly, giving dataset boosting a greater opportunity to improve things. However if the randomly deleted columns are simply noise we expect it to be harmless to baseline model performance and dataset boosting will just add further noise.
The pattern that can be seen in most of the graphs is an asymmetric benefit to using this new boosting scheme. When boosting improves performance, it does so by a large margin. When it hinders performance it's mostly by a much smaller margin.
The only exception here is tabular_playground where it underperfors in all cases. It is interesting to note that on this dataset - unlike all the
others I'm using - logistic regression performs as well as gradient boosting. It is fairly easy to prove that when a linear model works there is no advantage to boosting, so this should not
be surprising.
| scenario | win_base | win_new_only | delta_base | delta_new_only | boosted_regret | base_regret | new_only_regret |
|---|---|---|---|---|---|---|---|
| car_insurance | 0.600 | 0.633 | 0.016 | 0.006 | 0.011 | 0.028 | 0.017 |
| cover_type_dataset_shift | 0.989 | 0.378 | 0.014 | -0.000 | 0.003 | 0.016 | 0.003 |
| santander | 0.500 | 0.744 | 0.011 | 0.010 | 0.008 | 0.019 | 0.018 |
| synthetic_1 | 0.789 | 0.856 | 0.008 | 0.018 | 0.007 | 0.014 | 0.024 |
| synthetic_2_dataset_shift | 0.911 | 0.844 | 0.015 | 0.015 | 0.018 | 0.033 | 0.033 |
| tabular_playground | 0.056 | 0.522 | -0.015 | 0.000 | 0.017 | 0.001 | 0.017 |
The columns win_base and win_new_only represent the fraction of times when my dataset boosting scheme outperforms training the model on either
the full dataset (win_base) or the new rows only (win_new_only). Thedelta_base/delta_new_onlycolumns represent the average lift.
Finally, the?_regret` columns represent the difference in performance between a model trained on the full dataset (i.e. without dropping any data)
and the model trained on the censored dataset. This is averaged across all simulations.
Relevance of the censored features
A natural question arises - how does the benefit of dataset boosting relate to the importance of the features that are missing in the old data?
The meaning of importance: It is important to clarify that by "importance", I mean the importance of the features to a model trained
on full uncensored data. I have evaluated this by training a model on the full data (the same ones used to compute regret) and then using
sklearn.inspection.permutation_importance to compute the importance of each feature.
Some reasoning:
- As the importance of the censored features increases we would expect the benefit of boosting relative to training on the full dataset to increase. This is because in the full model (trained on all data), the fraction of the dataset which contains the high importance features is very low. Whereas in the boosted model, we have constructed a model so that these features are treated as if they are fully available, which they are.
- As the importance of uncensored features decreases, we would expect the base model (trained on censored data only) to provide little/no useful information. hus, in this situation, the model trained on new data only become the "best possible" model and the dataset boosting scheme will simply be adding noise.
To test this theory I ran a similar simulation to what is described above. However this time I kept the fraction of the dataset which is old constant (at 85%) while varying the number of features which were dropped.
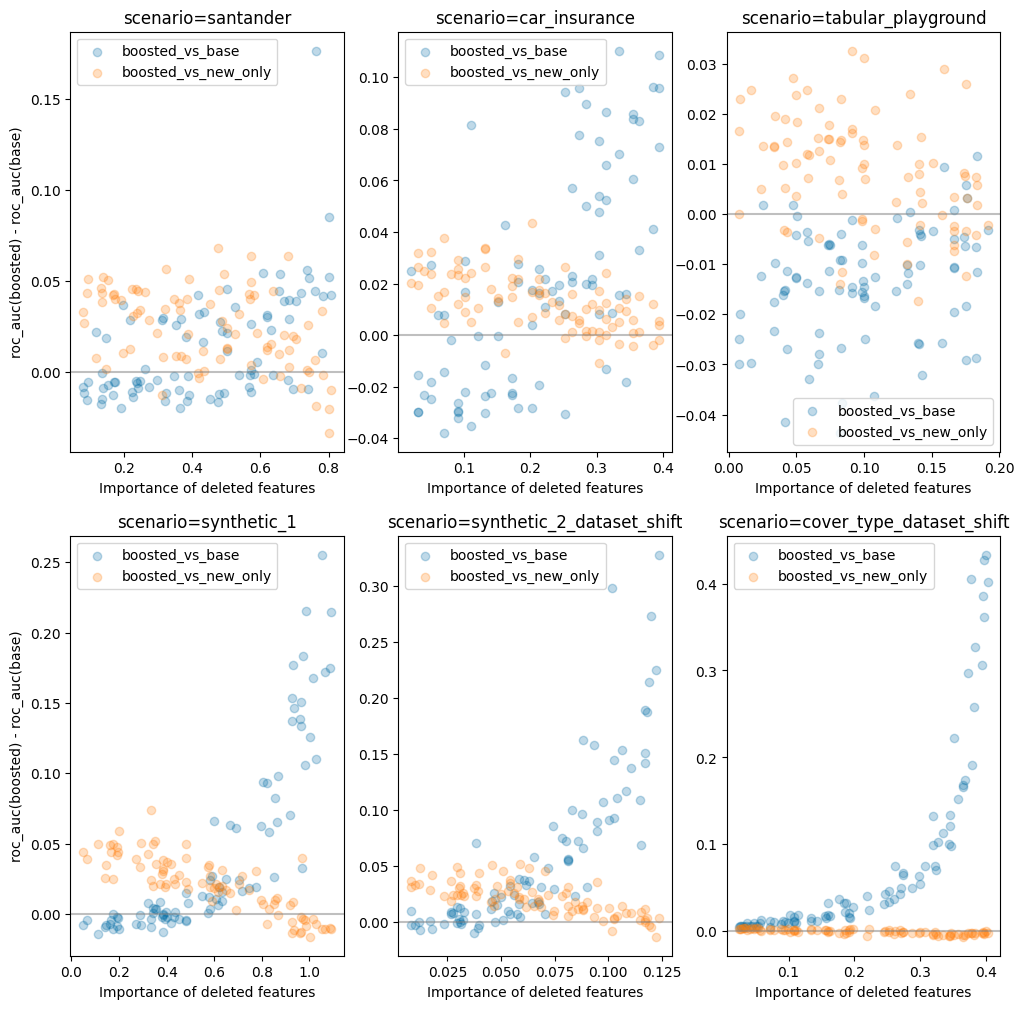
As can be seen, on most datasets for which boosting is helpful, the pattern I speculated about above does seem to hold out.
Conclusion
In many of the simple examples I've tested it with here, this boosting scheme seems to be a significant improvement over the most obvious alternative approaches.
Dataset boosting is generally beneficial when:
- The old data comprises a large fraction (80% or more) of the dataset.
- The new data is not large enough to train an accurate model by restricting solely to the new data.
- The features present in the old data and the features missing from the old data both have significant importance.
It is not beneficial in other cases and mostly seems to add noise, diminishing accuracy.
This shouldn't be very surprising since the theoretical justification and practical applicability of boosting has been known for a long time. But nevertheless, I've not seen this approach used to address issues related to dataset completeness, and I'm hoping a kind reader might point me to a body of literature addressing this or persuade someone to research this in greater generality.
Related
- Adapted Tree Boosting for Transfer Learning, some Alipay guys using a similar idea for a somewhat different purpose.
- Multiclass adaboost original paper on the topic.