So I've just launched my new startup, BeerBnB. It's a hip little site matching beer drinkers with specialty microbreweries - AirBnB for drinkers, or maybe eBay for brewers. My ~~marketer~~ growth hacker has gotten some early publicity by advertising in the bathroom of a few bars - the result was 794 unique visitors of whom 12 created an account. Doing some division I've computed an empirical conversion rate of 12/794=1.5%.

To begin with, this seems promising. A 1.5% conversion rate isn't great, but it's certainly enough to get started. Investors have suggested that they will probably invest if the conversion rate exceeds 1%.

Now, suppose the marketer has the ability to get a lot more publicity. He can expose BeerBnB site to approximately 10,000 visitors via toilet adds at bars around the city. Suppose we make the assumption that these 10,000 visitors will convert at the same rate as the 794 early visitors. How many people can I reasonably expect to signup? This isn't a trick question - the expectation is about 150 signups. But how confident are we that we will really see 150 signups? How confident are we that the conversion rate is higher than 1%?

The answer to this question is a fairly straightforward exercise in Bayesian reasoning. But I'm going to be a bit pedagogical, and use this blog post as a jumping off point for explaining Bayes rule in practice. This is also a prelude to future posts, where I'll explain how to use Bayesian reasoning for A/B testing and Bandit Algorithms.

Bayesian Basics

The first important concept in Bayesian reasoning is the underlying model. In our case, we take a very simple model. We assume there exists an (unknown) parameter $@\theta \in [0,1]$@. A unique visitor to the site will create an account with probability $@\theta$@ - i.e., $@\theta$@ is our true conversion rate.

In Bayesian reasoning, the fundamental goal is to compute a posterior distribution on $@\theta$@. This means we want to find a function $@f(x)$@ with the property that:

$$ P( a < \theta < b) = \int_a^b f(\theta) d\theta $$

In graphical terms, the probability that $@a < \theta < b$@ can be interpreted as the area under the curve of the graph of $@f(\theta)$@:

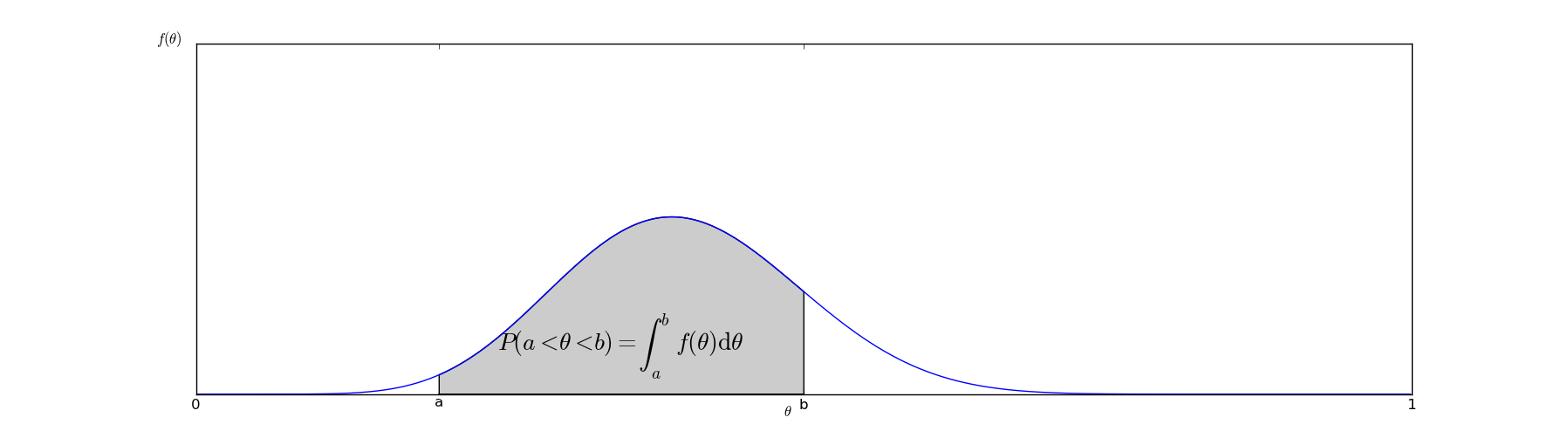
graph of posterior distribution

The function $@f(x)$@ represents our beliefs about $@\theta$@ - it is an inherently subjective matter. It depends on our beliefs about what typical values of $@\theta$@ might be as well as the evidence we have seen. What Bayesian analysis provides us with is an objective method of altering $@f(x)$@ based on the evidence we have about it.

Why do we care?

Given the posterior distribution, we can come up with many useful conclusions. For example, given $@f(x)$@, it is relatively straightforward to compute credible intervals. Suppose we can find $@a$@ and $@b$@ so that:

$$ \int_a^b f(\theta) d\theta > 0.95 $$

This means we are confident with 95% certainty that the true value of $@\theta$@ lies somewhere between a and b. Actually computing these $@a$@ and $@b$@ is relatively straightforward from a computational perspective. One straightforward algorithm for doing this is to start with $@a=b$@ and incrementally move them apart, stopping only when we achieve 95% confidence.

We can also compute our expected number of user signups:

$$ \int_a^b \textrm{number of unique visitors} \cdot \theta f(\theta) d\theta$$

In fact, almost any question we want to answer can be computed by doing computations against $@f(\theta)$@.

Updating our beliefs with Bayes rule

As you might expect, Bayes rule plays a crucial part in changing our beliefs based on evidence. As a refresher, Bayes rule states that:

$$ P( fact | evidence) = \frac{ P(evidence | fact) P(fact) } { P(evidence) } $$

To use Bayes rule in our context, we simply need to plug our model into this formula. In our context, the fact we want to compute the probability of the true conversion rate being $@\theta$@.

Recall that the evidence we have is that we ran 794 trials and observed 12 conversions. Assuming that we knew $@\theta$@, what would the probability of actually observing that result be? The answer to this is an exercise in elementary statistics - we need only use the Binomial Distribution:

$$ P( \textrm{12 page views, 794 visitors} | \theta ) = { 794 \choose 12 } \theta^{12}(1-\theta)^{794-12} $$

Now, what about computing $@P(fact)$@? Unfortunately, there is no easy answer to this. We can't actually compute this function at all - $@P(fact)$@ is our prior distribution, and is purely a subjective choice. What $@P(fact)$@ represents is our beliefs before we have gathered any evidence. The need to choose a prior is one of the two major sources of subjectivity in Bayesian reasoning - the other source of subjectivity is the underlying choice of model.

When choosing a prior, there are two major considerations. The first is mathematical simplicity - why make our calculations harder than they have to be? The second is that we don't want our initial beliefs to be too strong, otherwise evidence may never overcome them.

Choosing priors - two approaches

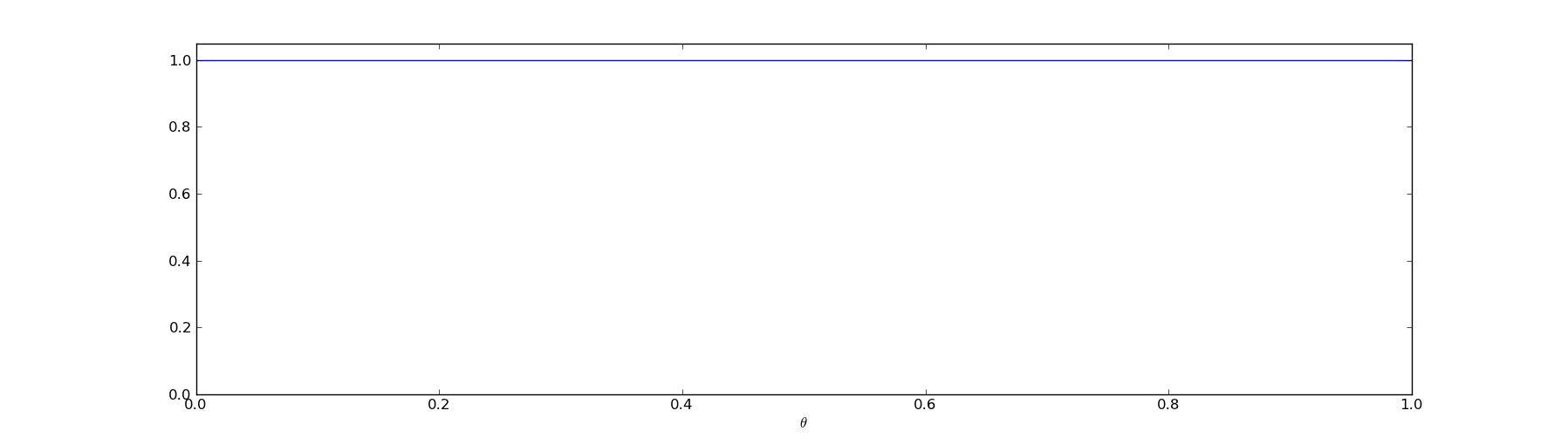
The most obvious prior we could choose for the problem of conversion rates is the uniform prior. This means that all values of $@\theta$@ are equally likely. This is a minimally informative prior - it gives us as little information as possible, so we need to depend exclusively on the evidence.

graph of prior distribution

The other prior we could choose is based on our intuition about website conversion rates - in general, they tend to be low. A conversion rate larger than 10% is extremely unlikely - it's more likely we made a mistake than we actually observe a 50% conversion rate. In this case, we would want to choose a prior that looks something like this:

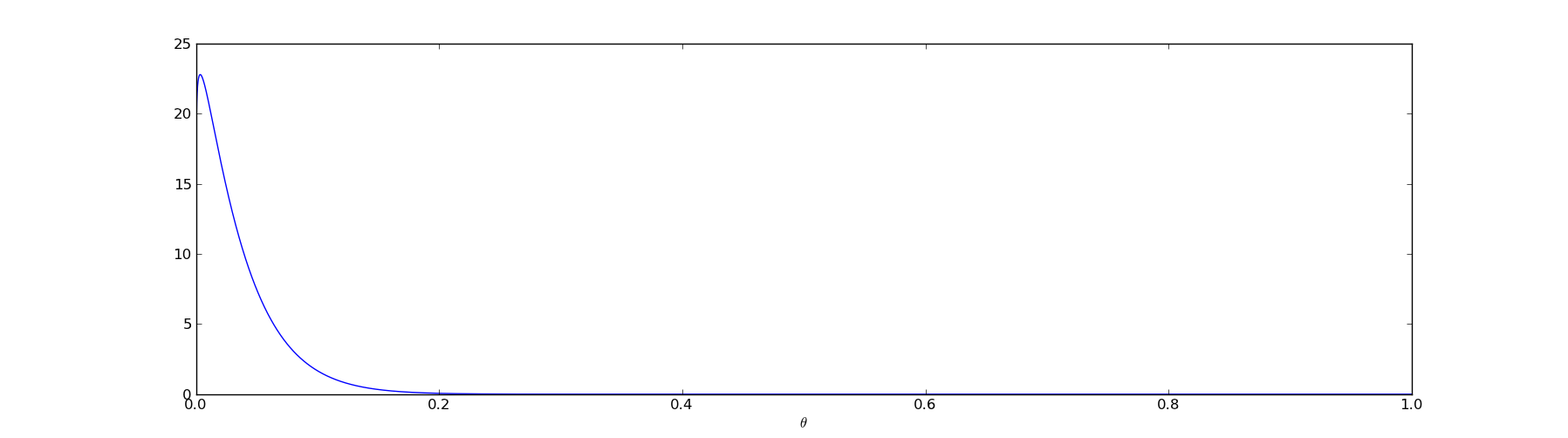
graph of prior distribution

This prior says that although the true value of $@\theta$@ is unknown to us, we are almost certain it is smaller than 0.1.

Since I believe that conversion rates are typically smaller than 10%, I'll go ahead and use the informative prior. But the analysis I'm about to do could still be repeated with the uniform prior.

A mathematically simple prior

As a way to precisely define the prior, I will choose the beta distribution:

$$ f_{\alpha, \beta}(\theta) = \frac{ \theta^{\alpha-1} (1-\theta)^{\beta-1} }{ B(\alpha, \beta) } $$

I'm only choosing the beta distribution specifically for mathematical simplicity. The beta distribution will allow me to short circuit a bunch of algebra later, but conceptually it is nothing special. In principle, I could just as easily use other similar looking functions, the algebra would just be more tedious.

Specifically, I'll take as the prior $@f_{1.1,30}(\theta)$@, which is the function I graphed in the previous section.

In this formula, $@ B(\alpha,\beta) = \int_0^1 t^{\alpha-1}(1-t)^{\beta-1} dt $@ is the standard [Euler beta function](https://en.wikipedia.org/wiki/Beta_function). The only purpose of the $@B(\alpha,\beta)$@ term is normalization, understanding it is not important to the final analysis.

Putting the pieces together

Warning: A significant chunk of algebra lies ahead. Feel free to skip straight to the conclusion if you want.

Remember again that Bayes rule says:

$$ P( fact | evidence) = \frac{ P(evidence | fact) P(fact) } { P(evidence) } $$

Plugging in our objective calculation of $@P(evidence | fact)$@ and our subjective choice for $@P(fact)$@, we obtain:

$$ P( \theta | \textrm{12 page views, 794 visitors} ) = \frac{ { 794 \choose 12 } \theta^{12}(1-\theta)^{794-12} f_{1.1, 30}(\theta) }{ P(evidence) } $$

We can separate out from this all constants - the pieces which don't vary with $@\theta$@:

$$ P( \theta | \textrm{12 page views, 794 visitors} ) = { 794 \choose 12 } \frac{ 1}{ P(evidence) B(1.1,30) } \theta^{12+1.1-1}(1-\theta)^{794-12+30-1} $$

Or, written more simply:

$$ P( \theta | \textrm{12 page views, 794 visitors} ) = \frac{ \theta^{12+1.1-1}(1-\theta)^{794-12+30-1} }{ C }$$

If you skipped the math, start reading again.

It turns out that $@C = B(12+1.1,794-12+30)$@, although I'm going to skip the algebra which proves this (you can find it here if you want to see). This means that our posterior distribution is:

$$ P( \theta | \textrm{12 page views, 794 visitors} ) = f_{1.1+12, 30+794-12}(\theta) $$

I.e., the posterior is just another beta distribution, albeit with different parameters. In the next picture I'll plot the prior (the blue line) together with the posterior (the green line) to illustrate how the evidence has shaped our beliefs:

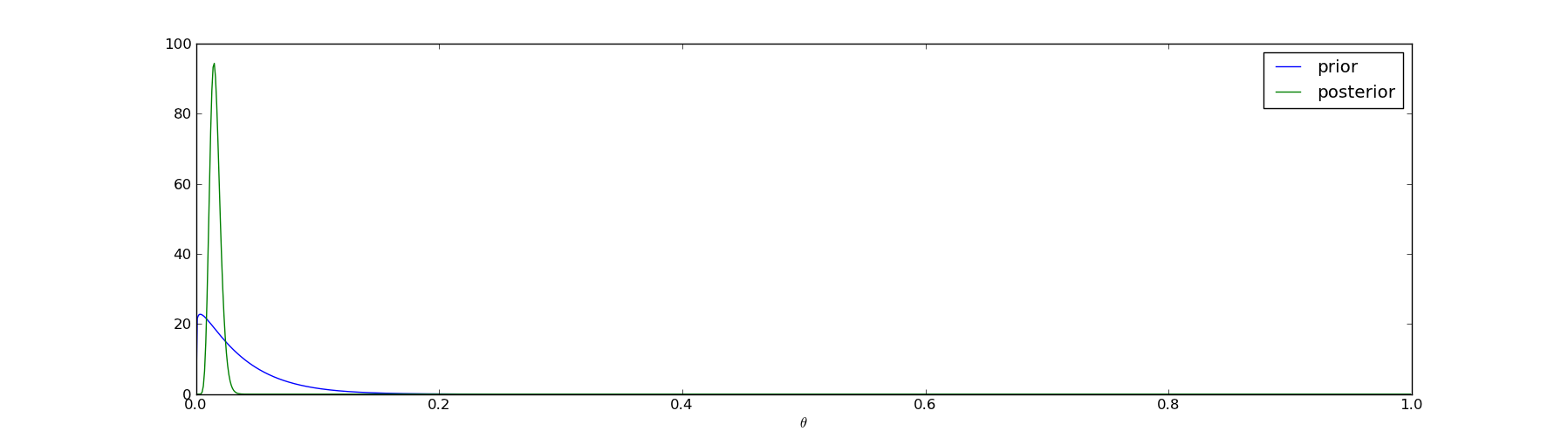
graph of posterior distribution

The interesting part of the posterior graph is the range $@\theta \in [0,0.1]$@, so we can zoom in to that region (and graph only the posterior):

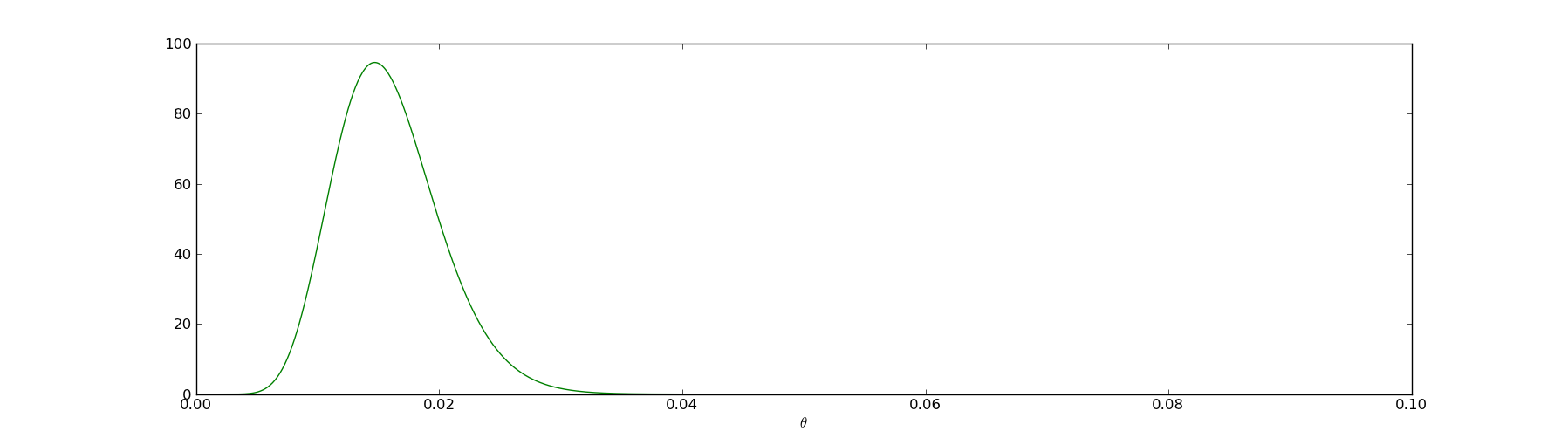
graph of posterior distribution

More generally, suppose that for any problem of this nature we choose the prior $@f_{\alpha,\beta}(\theta)$@. Then suppose we gather evidence by running N trials and observe K successes. The posterior is:

$$ \textrm{posterior} = f_{\alpha+K, \beta+N-K}(\theta) $$

So what is the conclusion?

First of all, we have our credible intervals. We are virtually certain that the true conversion rate $@\theta \in [0.005, 0.03]$@. Unfortunately that's a pretty wide range - it's possible that our conversion rate is nearly zero and we only signed up 12 visitors via a fluke.

We can also compute the possibility that the conversion rate is at least 1%::

$$ \int_{0.01}^1 f_{1.1+12, 30+794-12}(\theta) d\theta = 0.93127 $$

This was computed by me with the following python code, which I'm going to display simply to emphasize that manipulating these variables in python/scipy is quite simple:

from pylab import *
from scipy.stats import beta

dx = 0.0001
x = arange(0.01,1.0,dx)
result = beta(1.1+12, 30+794-12).pdf(x).sum()*dx
print result

That's fairly good news - the odds are more than 93% that our conversion rate is above 1%. Sounds like it's time to go talk to investors.

What if we chose a different prior?

After deciding to seek investment, I managed to get a meeting with Cuba Thielion, the legendary VC who owns sports teams and funds Bayesian analysis. He is a very smart guy and certainly the sort to be persuaded by statistical evidence. But as I'm presenting my analysis and demonstrating why I believe conversion rates exceed 1%, he immediately pokes a hole in it: "Your prior is really strong. How do you know what typical conversion rates are in general? I think you should assume nothing about the prior distribution and just pick a uniform prior."

His concern is that I'm assuming too much about about the distribution of $@\theta$@. My analysis was certainly effective in convincing me that I am likely to have at least a 1% conversion rate. But how can I convince him?

The answer is pretty straightforward - I should perform the same analysis, but use his prior beliefs rather than mine. He likes the uninformative prior, which corresponds to a beta distribution with $@\alpha=\beta=1$@. So instead of using the prior $@f_{1.1,30}(\theta)$@, I instead use $@f_{1,1}(\theta)$@ and repeat the calculations I performed above.

The result is graphed here:

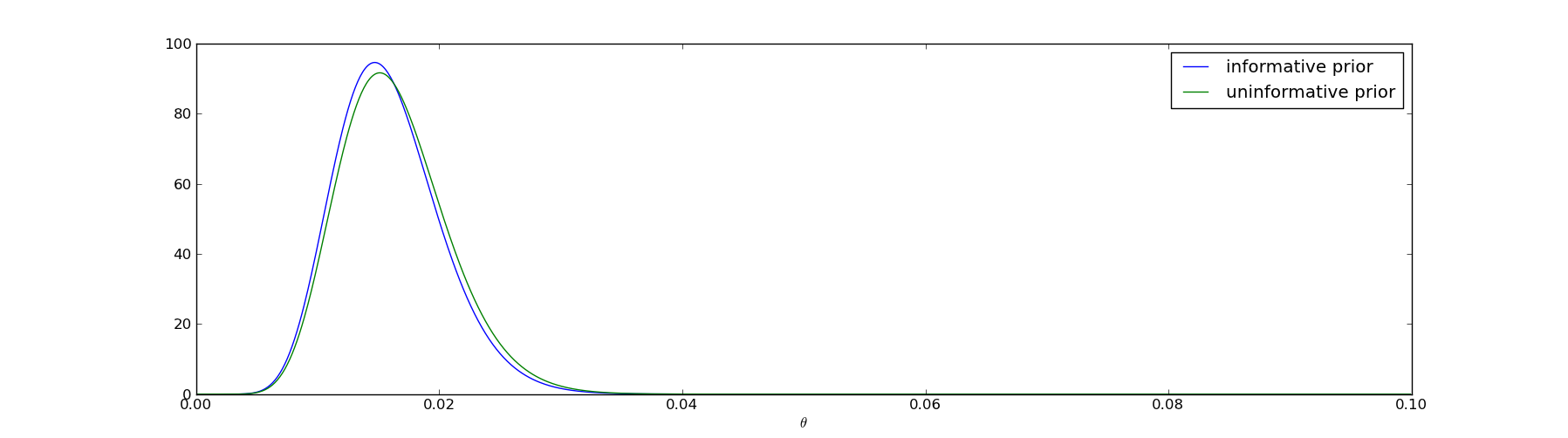
graph of posterior distribution

The two posteriors differ, but not very much. Cuba Thielion, being a perfectly rational Bayesian, is immediately convinced that you will achieve a 1% conversion rate.

Where to go next

In this post I haven't done anything particularly impressive. All we've done is shown how to measure conversion rates using Bayesian methods.

If you want to optimize click through/conversion rates, you can read about the Bayesian Bandit which allows you to increase your click through rate in realtime.

What if your conversion rates vary with time? This blog post provides one method for measuring them based on the same ideas here.

Bayesian Basics

Why do we care?

Updating our beliefs with Bayes rule

Choosing priors - two approaches

A mathematically simple prior

Putting the pieces together

So what is the conclusion?

What if we chose a different prior?

Where to go next

Subscribe to the mailing list