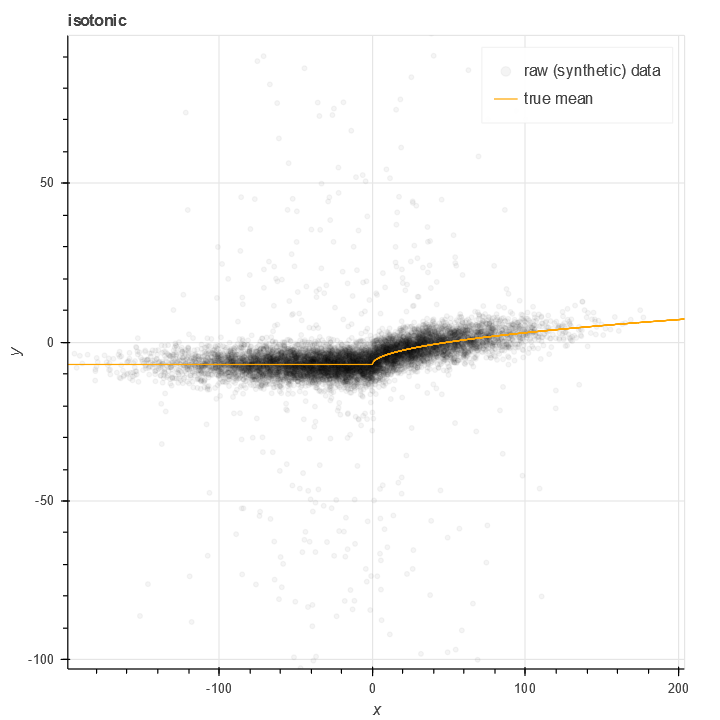
Boosting as a scheme for transfer learning
Here's a scenario that I believe to be common. I've got a dataset I've been collecting over time, with features \(x_1, \ldots, x_m\) This dataset will generally represent decisions I want to make at a certain time. This data is not a timeseries, it's just data I happen to have …
more ...